Variance of a random variable

Take a random variable \(X\) (either continuous or discrete). Assume that the expectation is some number:

\[ \mu = \mathbf{E}[X]. \]

The variance \(\mathbf{V}[X]\) of \(X\) is defined as the expectation of the squared difference of \(X\) from the expected value (or the mean) \(\mu\), i.e.,

\[ \mathbf{V}[X] := \mathbf{E}\left[(X-\mu)^2\right]. \]

You can think of the variance as the measure of the spread of the random variable around its expected value. See variance_comparison_1 and variance_comparison_2 for a visualization.

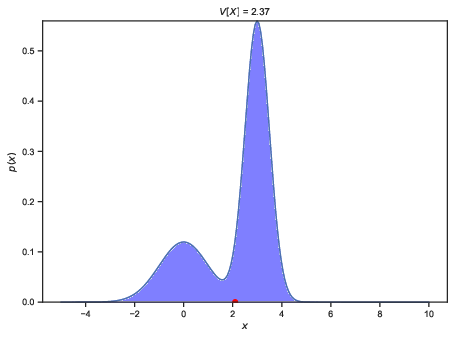
The variance is always positive. If \(X\) has units, then the variance of \(X\) has these units squared. For example, if \(X\) is in meters, then \(\mathbf{V}[X]\) is in meters squared. Very often, instead of the variance we use the standard deviation of a random variable. The standard deviation is defined to by the square root of the variance:

\[ \sigma := \sqrt{\mathbf{V}[X]}. \]

The standard deviation is more convenient because it has the same units as \(X\). But its intuitive meaning is the same.