.md .pdf

Probability of logical disjunctions

All other rules of probability theory can be derived from the two basic rules. So take two logical propositions \(A\) and \(B\). The logical disjunction of \(A\) and \(B\) is the logical proposition (\(A\) or \(B\)). In our notations we write \(A + B\) for (\(A\) or \(B\)) We can deduce from the basic rules of probability that:

\[ p(A + B|I) = p(A|I) + p(B|I) - p(AB|I). \]

In words, this says

The probability of A or B is the probability that A is True plus that probability that B is true minus the probability that both A and B are True.

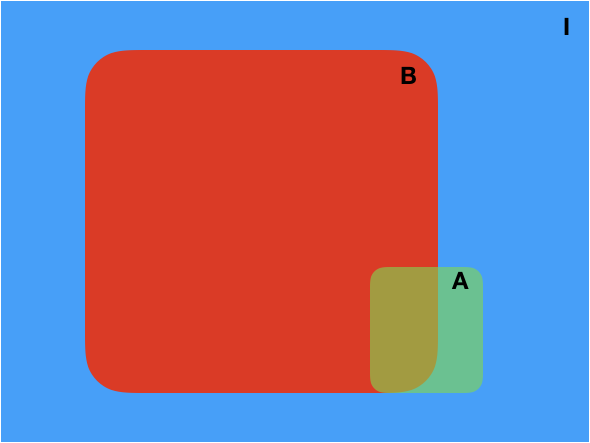
Fig. 5 Venn diagram showing the information \(I\), and the logical propositions \(A\) and \(B\).

This is very easy to understand intuitively by looking at the Venn diagram. Fig. 3. The probability \(p(A+B|I)\) is the area of the union of A with B (normalized by I). This area is indeed the area of A (normalized by I) plus the area of B (normalized by I) minus the area of A and B (normalized by I) which was double-counted.

Let’s see a formal proof of this:

\[\begin{split} \begin{split} p(A+B|I) &=& 1 - p(\neg (A+B)|I)\\ &=& 1 - p(\neg A, \neg B|I)\;\text{(obvious rule)}\\ &=& 1 - p(\neg A|\neg B, I)p(\neg B|I)\;\text{(product rule)}\\ &=& 1 - \left[1 - p(A|\neg B, I)\right]p(\neg B|I)\;\text{(obvious rule)}\\ &=& 1 - p(\neg B|I) + p(A|\neg B, I)p(\neg B|I)\\ &=& 1 - p(\neg B|I) + p(A\neg B|I)\;\text{(product rule)}\\ &=& 1 - p(\neg B|I) + p(\neg B|A,I) p(A|I)\;\text{(product rule)}\\ &=& 1 - p(\neg B|I) + \left[1 - p(B|A,I)\right]p(A|I)\;\text{(obvious rule)}\\ &=& 1 - p(\neg B|I) + p(A|I) - p(B|A,I)p(A|I)\\ &=& 1 - \left[1 - p(B|I)\right] + p(A|I) - p(B|A,I)p(A|I)\;(\text{obvious rule})\\ &=& p(A|I) + p(B|I) - p(B|A,I)p(A|I)\\ &=& p(A|I) + p(B|I) - p(AB|I)\;\text{(product rule)}. \end{split} \end{split}\]

previous

Example - Drawing balls from a box without replacement

next

The sum rule