The sum rule¶

This is the final rule we are going to consider in this lecture. It is one of the most important rules. You absolutely have to memorize it. It goes as follows.

Consider the sequence of logical sentences \(B_1,\dots,B_n\) such that:

One of them is definitely true:

\[ p(B_1 + \dots + B_n|I) = 1. \]

They are mutually exclusive:

\[\begin{split} p(B_iB_j|I) = \delta_{ij} = \begin{cases}1,&\;\text{if}\;i=j,\\ 0,&\;\text{otherwise}.\end{cases} \end{split}\]

Then, for any logical sentence \(A\) we have:

\[ p(A|I) = \sum_{i=1}^n p(AB_i|I) = \sum_{i=1}^n p(A|B_i,I)p(B_i|I). \]

Again, this requires a bit of meditation. You take any logical sentence A and set of exclusive but exhaustive possibilities \(B_1,\dots,B_n\) and you break down the probability of \(A\) in terms of the probabilities of the \(B_i\)’s. The Venn diagrams in Fig. 6 can help you understand what is going on.

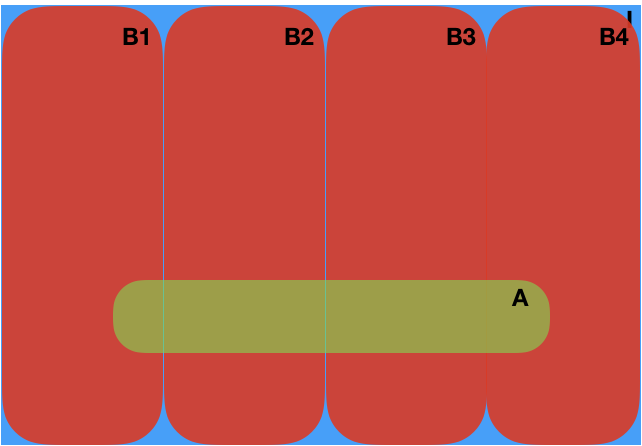
Fig. 6 Visualization of the sum rule of probability.¶

The sum rule can be trivially proved by induction using only the obvious rule and the product rule. It is instructive to go through the proof. For \(n=2\) we have:

\[\begin{split} \begin{split} p(A|I) &=& p(A\;\text{and}\;(B_1\;\text{or}\;B_2)|I)\\ &=& p\left((A\;\text{and}\;B_1)\;\text{or}\;(A\;\text{and}\;B_2)|I\right)\\ &=& p(A\;\text{and}\;B_1|I) + p(A\;\text{and}\;B_2|I) - p\left((A\;\text{and}\;B_1)\;\text{or}\;(A\;\text{and}\;B_2)|I\right)\\ &=& p(AB_1|I) + p(AB_2|I) - p(AB_1B_2|I)\\ &=& p(AB_1|I) + p(AB_2|I), \end{split} \end{split}\]

because

\[ p(AB_1B_2|I) = p(B_1B_2|I)p(A|I) \le p(B_1B_2|I) = 0. \]

And then, assume that it holds for \(n\), you can easily show that it also holds for \(n+1\) completing the proof.

Introduction to Data Science for Mechanical Engineers (Lecture Book)

The sum rule

The sum rule¶