The basic rules of probability¶

There are two rules of probability from which everything else can be derived. These are direct consequences of the desiderata and Cox’s theorem (see The common sense assumptions that give rise to the basic probability rules.). They are:

The obvious rule:

\[ p(A|I) + p(\neg A|I) = 1. \]

The product rule (or Bayes’ rule):

\[ p(AB|I) = p(A|BI)p(B|I). \]

I call it the first rule the “obvious rule” because it is obvious… It states that either \(A\) or its negation \(\neg A\) must be True. That’s trivial. A logical proposition about the world is either True or False.1 Let me stress again that it is vitally important that you do not try to apply probability in a system that includes contradictions.

The product rule is not obvious. Understanding it requires a bit of meditation. It states that the probability of A and B is the probability of A given that B is True times the probability that B is True. We can use the Venn diagram of Fig. 3 to understand what it all means.

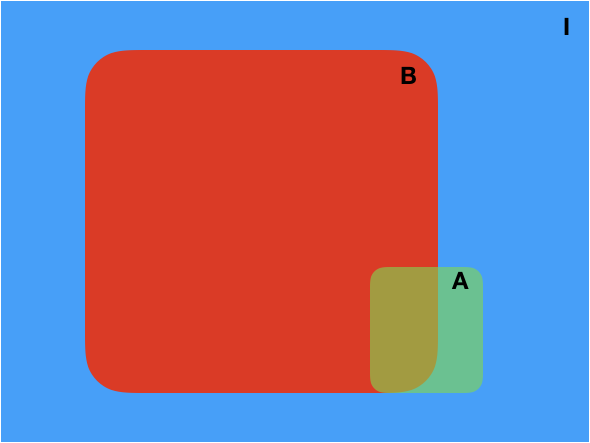
Fig. 3 Venn diagram showing the information \(I\), and the logical propositions \(A\) and \(B\).¶

You can think of a Venn diagram as a 2D representation of everything that can happen in the world. Each point inside the blue area is a possibility allowed by the information \(I\). The red area marks the possibilities in which \(B\) is True and the green area marks the possibilities in which \(A\) is True. The intersection of the red and the green area (brown) marks the possibilities in which both \(A\) and \(B\) are True.

In Venn diagrams probabilities correspond to normalized areas. It goes like this:

\[ p(\text{something} | \text{something else}) = \frac{\text{area of intersection of something and something else}}{ \text{area of something else}}. \]

Strictly speaking, this is not an equality but a correspondence or analogy. In our particular case, we have:

\[\begin{split} \begin{array}{ccc} p(B|I) &=& \frac{\text{area of intersection of}\;B\;\text{and}\;I\;\text{(red)}}{\text{area of}\;I\;\text{(blue)}}\\ &=& \frac{\text{area of}\;B\;\text{(red)}}{\text{area of}\;I\;\text{(blue)}}. \end{array} \end{split}\]

Similarly:

\[\begin{split} \begin{array}{ccc} p(A|BI) &=& \frac{\text{area of the intersection of}\;A\;\text{and}\;\text{B and}\;I\;\text{((brown)}}{\text{area of intersection of}\;B\;\text{and}\;I}\\ &=& \frac{\text{area of the intersection of}\;A\;\text{and}\;\text{B (brown)}}{\text{area of}\;B\;\text{(red)}}, \end{array} \end{split}\]

and

\[ p(AB|I) = \frac{\text{area of intersection of}\;A\;\text{and}\;\text{B (brown)}}{\text{area of}\;I\;\text{(blue)}}. \]

Thus, we have:

\[\begin{split} \begin{array}{ccc} p(AB|I) &=& \frac{\text{area of intersection of}\;A\;\text{and}\;\text{B (brown)}}{\text{area of}\;I\;\text{(blue)}}\\ &=&\frac{\text{area of intersection of}\;A\;\text{and}\;\text{B (brown)}}{\text{area of}\;I\;\text{(blue)}}\cdot \frac{\text{area of}\;B\;\text{(red)}}{\text{area of}\;B\;\text{(red)}}\\ &=& \frac{\text{area of intersection of}\;A\;\text{and}\;\text{B (brown)}}{\text{area of}\;B\;\text{(red)}}\cdot \frac{\text{area of}\;B\;\text{(red)}}{\text{area of}\;I\;\text{(blue)}}\\ &=& p(A|BI)p(B|I), \end{array} \end{split}\]

which is the product rule. Keep in mind that this is not a mathematical proof. However, it can help you develop a little bit of intuition about the product rule.

1: However, according to Gödel’s incompleteness theorem there some mathematical statements that are neither True nor False. These are also excluded.

Introduction to Data Science for Mechanical Engineers (Lecture Book)

The basic rules of probability

The basic rules of probability¶